Hyper Parameter 하이퍼파라미터
머신러닝, 딥러닝 기술을 배우고 구현할 때 가장 많이 접하게 되는 단어들 중 하이퍼파라미터(Hyper Parameter)가 있다.
직역하면 파라미터가 매개변수라는 뜻이므로 초매개변수라고 이야기들 한다.
Model이 Learning 할 때 효과를 좋게해줄 수 있는 변수로 Weight와 Bias 등과 같은 파라미터가 가닌 자동으로 설정되는 변수를 의미한다.
Hyper parameter는 아래와 같이 여러가지가 있다.
1. Hyper Paramters Related To Network Structure
우선 네트워크 구조와 관련된 하이퍼 파라미터들이 있다.
(1) Number of Hidden Layer and Units
Hidden Layer는 Input Layer와 Output Layer 사이의 계층으로 Hidden Layer의 갯수와 각각의 레이어들의 Unit=Neuron=Perceptron=Node 의 갯수 2가지가 변수가 된다.
보통 많은 각 은닉층의 뉴런들은 정규화 기술이 적용되며 모델의 정확도를 높이는데 기여한다. 그리고 뉴런의 갯수와 레이어의 깊이가 학습 시 Underfitting, Overfitting 에 영향을 준다.
(2) Dropout
Drop out은 overfitting을 피하기 위한 정규화 기법이다. 학습데이터에 과적합하게 학습된 model을 실제로 사용하기 위해 범용성을 위한 기법으로 Hidden Layer의 Neuron들을 일정 비율로 배제하고 학습을 한다.
Drop out의 Hyper Parameter은 neuron들 out시킬 비율이 되는데 이 확률이 낮으면 효과를 크게 얻지 못할 것이고, 값이 크면 Underfitting이 될 수 있다.
(3) Weight Initalization in Network
가장 이상적인 방법은 각 레이어에 사용되는 Activation function에 따라서 적절한 Weight 초기화 기법을 사용하는 것이 좋다.
Relu, Leaky Relu 등의 비슷한 계열의 Activation function들을 사용하면 He 초기화 기법을 사용.
초기화 시 사용되는 난수는 균등분포(uniform distribution)를 대부분 사용한다.
2. Hyper Paramters Related To Training Algorithm
학습에 사용되는 하이퍼 파라미터들은 학습 시 연산되는 값이나 속도, 횟수와 관련되 있다.
(1) Learning rate
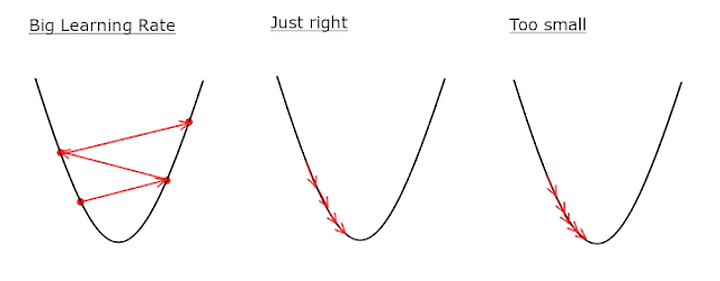
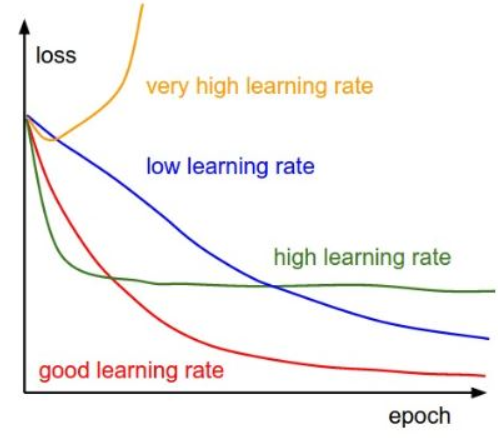
학습이란건 Error를 통해 최적의 Weight값을 찾아가는 것인데, 자세히 애기하면 model로부터 얻은 예측값(output)이 기대값(lable)과의 차이를 이용하여 얻은 cost값과 Weight 간의 Gradient 값을 이용하여 기존의 Weight를 Update하여 cost값이 Global minimum이 되는 지점을 찾아가게된다. 여기서 Gradient값으로 Weigh를 이동(Update)를 할 때 얼마만큼 이동할지 정하는 것이 Learning Rate이다.
Learning rate를 학습 속도, 걸음크기, Gap 등으로 표현하여 설명할 수 있으며, Learning Rate를 고정값으로 사용하거나 학습을 진행하면서 값을 변화시켜 효과적으로 Global minimum에 도달할 수 있게 해주며 이러한 기법을 Learning Rate Decay라고 한다.
값이 크다면 Global minimum에 도달하지 못할 수 있으며 너무 작으면 학습 시간이 오래걸려 model을 시스템에 적용하여 서비스하기까지 기간이 오래걸릴 수 있으므로 상황에 맞게 적절하게 사용해야된다.
(2) Momentum
모멘텀은 Gradient Descent에 대한 Optimization 기법으로 직역하면 탄성, 관성 등의 뜻으로 Global minimum에 도달하기위해 Learning하는 과정에서 Weight가 Update하는데 말그대로 관성, 가속도를 주어 Weight가 감소하거나 증가하는 방향으로 더 많은 변화를 주는 것이다.
모멘텀을 적용하는 이유는 Weight를 Update할때 관성을 주어 Cost-Weight 그래프에서 지그재그로 변화하는 횟수를 줄여 학습횟수를 줄이면서 Global minimum에 도달할 수 있게 해준다.
모멘텀은 Backpropagation에서 Weight update에 사용되는 헤브의 학습규칙(Hebbian Learning Rule)에서 Chain Rule의 결과값과 곱셈으로 추가하여 사용된다.
(3) Number of Epochs
학습을 반복하는 횟수가 하이퍼파라미터 중 하나이다.
Epoch란 model이 전체 Dataset에 대해 Feedforwarding, Backpropagation을 거친 것을 의미한다. 즉, 전체 데이터셋을 한번 학습을 완료한 상태이다.
학습을 많이하면 error가 낮아질것이라 예측할 수 있지만, validation 단계에서 error가 감소하다가 어느 순간부터 다시 증가할 수 도 있다. 이 현상은 알다시피 overfitting이며 이로 인한 error를 다시 줄여주기 위해 epocj의 경계값을 찾는 것이 중요하며 상황에 따라 early stopping(조기종료)를 하여 과적합을 방지하는 것이 중요하다.
(4) Batch Size
Batch size는 한 번의 batch마다 주는 데이터 샘플의 size로 전체 Dataset을 한번에 학습하기에 하드웨어 시스템에 부담/한계가 되거나 시간상에 문제가 있을때 전체 Dataset을 일정 크기로 나눠 학습을하는데 여기서 나눠진 일정크기가 Batch Size가 된다. 보통 batch를 mini batch라고도 표현하며 나눠진 데이터셋을 뜻한다.
Batch size는 쉽게 말해 어떤 size로 Dataset을 나눌지 결정하는 크기이며 mini batch는 같은 크기로 전체Dataset을 나눈 Dataset들이다.
Epoch를 전체 Dataset을 1회 학습한다고 했는데 Batch size로 나눠진 mini batch들을 전부 다 학습하여 전체 Dataset을 1epoch 학습하는데 실행한 횟수를 Iteration이라고 한다.
Total Dataset = Batch Size x mini batch
1 Epoch = Batch Size x Iteration
(5) Cost function
기댓값 Label과 예측값 output의 차이를 Loss, Cost, Error 등으로 불려지는데, 이 차이를 구하는 여러 가지 방법들이 있다. 대표적인 방법인 Least Mean Squre 기법이나 Cross-entropy 등이 있다.
(6) Regularization Parameter
머신러닝의 목적은 error를 최소화하여 최적의 Weight를 찾는 것으로 이 학습과정에서 자주 등장하는 overfitting을 피하기 위해 L1, L2 Regularization 을 사용하여 이에 사용되는 변수는 Weight Decay의 속도를 조절하는데 사용할 수 있다. 이 가중치에 곱해지는 변수 또한 하이퍼 파라미터가 된다.
** 출처 **